This post is part of the How to… series
A problem frequently encountered when mapping structurally deformed rocks is deciding whether the fold you see in outcrop is part of a larger structure – an anticline or syncline, overturned or recumbent, plunging? The problem is exacerbated if stratigraphic facing (younging) criteria are absent or ambiguous. Fortunately, there is a solution to the problem based on fold asymmetry.
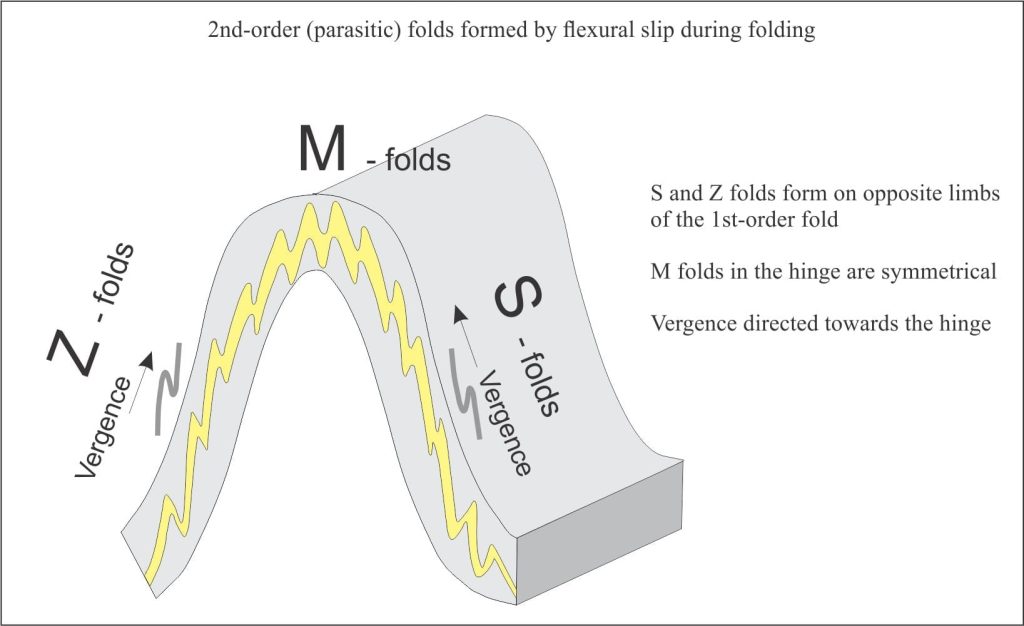
Large folds commonly have smaller-scale folds in their limbs and crest. They are usually referred to as higher-order (2nd, 3rd order etc.) or parasitic folds. They form during flexure of layered rock where slip occurs between rock layers – a mechanism called flexural slip. Structural geology teachers frequently use a soft-cover book to demonstrate this mechanism; bend the book into a fold and watch the slip between adjacent pages that is required to accommodate extension on the outer arc of the fold and shortening on the inner arc.
Parasitic folds are common in deformed sedimentary rocks where slip takes place along bedding planes or between layers with contrasting strength, such as mudstone and indurated sandstone (mudrocks have abundant clays and micas that are prone to slip and shear). The example below shows an anticline (1st-order structure) and smaller 2nd-order folds developed in a relatively weak layer. The 2nd-order folds have asymmetries related to the sense of slip on each fold limb and are called S- and Z-folds. Note that the 2nd-order M-folds in the hinge are symmetrical and in this example, upright.
The difference between S- and Z-folds lies in their sense of rotation, or vergence. The long limbs of S-folds are connected by a shorter limb that implies counter-clockwise rotation or sense of displacement; the opposite applies to Z-folds. Thus, the vergence of parasitic folds is towards the hinge line (or zone)
S- and Z-folds are three dimensional structures and will have hinge lines (or fold axes if we consider them to be cylindrical folds) and axial surfaces that can be measured. Another important property of parasitic folds is that their hinge lines (or fold axes) are parallel (or approximately so) to the hinge line of the 1st-order fold.
A note of caution; the sense of fold rotation-displacement will change if a fold is viewed from the opposite direction (i.e. S-folds will appear as Z-folds). Hence it is necessary to indicate the direction in which observations are made. Where possible, folds should be viewed down-plunge.
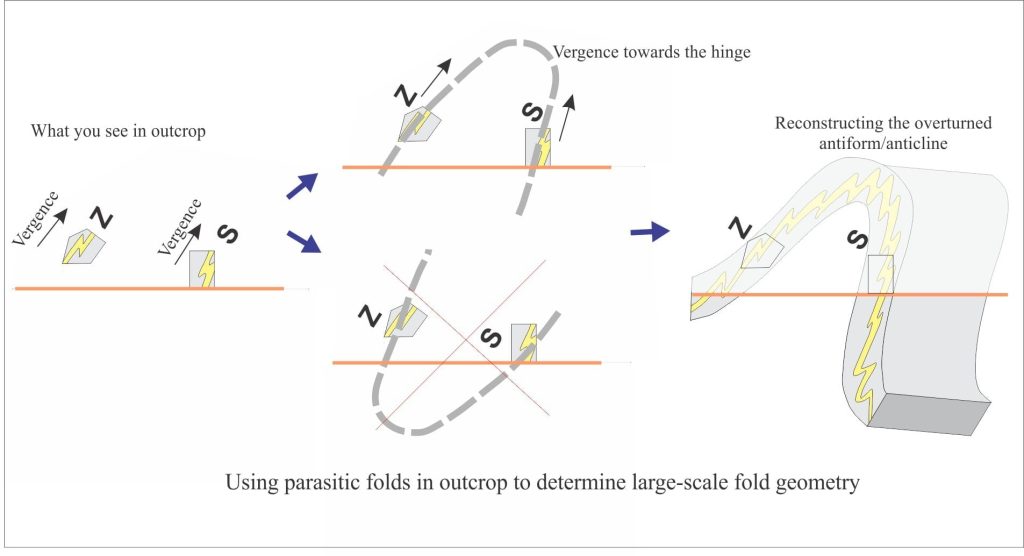
The geometric disposition of S- and Z-folds is extremely useful for deciphering large-scale folds, particularly when exposure is incomplete (as is commonly the case). The diagram below shows a scenario, where small folds are exposed in two outcrops.
Our view indicates the left outcrop is a Z-fold; the one on the right an S-fold. We can also determine the general attitude of the 1st-order fold limbs from dips and strikes on associated beds. If 1st-order fold-closure is beneath the surface, then it is a syncline (or synform if we don’t know facing direction); if above, an anticline or antiform. Both parasitic folds indicate vergence above the outcrops. If the structure was a syncline then the vergence should be in the opposite direction. The structure is therefore an antiform. If we have good facing direction data we could confirm the 1st-order structure is an overturned anticline (stratigraphy in the right outcrop is overturned).
Some other posts in this series:
Stereographic projection – the basics
Stereographic projection – unfolding folds
Stereographic projection – poles to planes
Faults – some common terminology