A measure of the universe; Renaissance slide-rules and Heavenly spheres

Measurement is a cornerstone of science, in fact of pretty well everything we do: How far? How fast? How long?  We take most measurement for granted, with little thought to how the process originated.  We demand accuracy and precision, forgetting that these are relatively modern luxuries.  Before the universal clock chimed GMT in 1884, there were more than 200 time zones in the US.  A league in France was shorter than a league in Spain, a discrepancy for which the 16^th C French scribe François Rabelais had an imaginative, if rollicking explanation.  In his tale, The Life of Gargantua and Pantegruel (1532-1564), a king required a standard distance to be determined (after all, if he was going to send his armies to battle it would be best if his advisors new how far they had to go).  He sent a trusted Knight, instructing him to ride to Spain, stopping every league to “roger and swive”; hence the discrepancy.  The leagues gradually became longer. The amusing satire of this explanation had its roots in real Medieval measures; the width of a hand, the distance one could walk in an hour.

By the end of the 16^th Century, with bourgeoning Renaissance creativity and inventiveness, the guess-work of measurement came to an end.  Measuring instruments were invented, craftsmen’s skills were honed. Wander through the Museo Galileo in Florence, through rooms filled with collections of mechanical devices (the Medici Collection is particularly important), and you are immediately struck, not only by the inventiveness, but also the consummate skill of the instrument makers.

One measuring device that stands out is Galileo’s Compass. There is some debate whether he alone invented this, or (unknowingly) shared the honours with Thomas Hood, an English mathematician. But Galileo’s version, the Proportional, or Sector Compass that was first constructed in 1597, became the standard for a multitude of arithmetic calculations; multiplication and division, square and cube roots, volumes and areas, trigonometric functions, latitudes, and parabolic distances for ballistics – a veritable slide-rule. Apart from the inquisitiveness of people like Galileo or Hood, a major driving force for accuracy of measurement was the military (not much has changed).

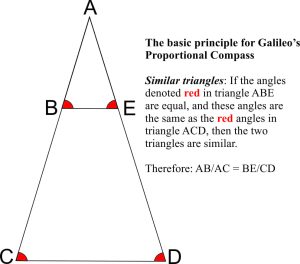The compass comprised two hinged legs, each carefully inscribed with several different scales.  The basic calculations were based on the proportionality of similar triangles, a simple yet powerful geometric relationship. Galileo went into business selling these instruments and providing lessons on their use.

Fifteenth and sixteenth century instrumentation wasn’t confined to earthly pursuits. Mounted globes, often beautifully adorned, mapped the celestial spheres; the ecliptic (the sun’s path), the fixed and wandering stars, always based on a fixed earth. Despite the persuasive efforts of Copernicus and Galileo, most mappers adhered rigidly to the Ptolemaic, earth-centred system, in part because they feared the consequences of promoting the alternative world-view.  The globes themselves are beautiful objects despite their cosmological construct.

Renaissance imagination, not satisfied with static globes, popularised a device with moveable, heavenly spheres; the Armillary Sphere (it was probably invented in China about the 3^rd to 1^st centuries BC, or ancient Greece, or both).  Armillary spheres attempted to map the heavens in three dimensions. They were only intended for illustration rather than measurement, but as such they represented attention to detail, and wonderful craftsmanship.

Armillary spheres became the thing to have in your living room.  Portraits of important people frequently showed the subject resting an arm on a sphere, where such objects were intended to signify a sense of faith, wisdom, knowledge, and perhaps above all, power.  The largest sphere, standing more than three metres high, was made for Ferdinand I de’ Medici by Antonio Santucci; it took 5 years to complete (1593). The sphere itself, about two metres in diameter, has the earth fixed at its centre. Seven spheres in succession represent the Moon, Mercury, Venus, the Sun, Mars, Jupiter, and the outermost wandering star, Saturn. An eighth sphere guides the viewer to the fixed stars, that includes a band locating the signs of the Zodiac. A ninth sphere, called the Prime Mover, encloses all other spheres; it also contains wire meridians.   All these spheres could be moved. The entire structure was framed by painted, circular wood supports that converge at the two poles, and represent great circles. A golden orb is mounted at the apex, on which a cross signifies the pinnacle of the heavenly sphere. A central iron rod holds it all together. A handle rotated the spheres so that an observer could witness the relationships among planets, stars, and the sun relative to Earth.

Surviving correspondence between Santucci and Galileo, indicates that Santucci had, after completing his sphere, second thoughts about his geocentric view of the universe.  Maybe he thought the evidence for it was unassailable.  But before he died, he reverted to his original world view. Did he fear eternal damnation? Or was he not able, intellectually or emotionally, to make the paradigm shift that would displaced him from the centre of everything.  Fast forward 500 years, and the conflicts between science,  belief systems and deep-seated ideologies, still simmer.