Geological models: An introduction

The posts in this series focus on Earth science models, particularly the soft-rock kind.

I have an abiding memory of my grandfather’s workshop. It was accessed through a trapdoor from the living room then a ladder to the basement. The entrance reflected his past as a sailor and shipwright. You knew you had arrived – the smell of cut timber and glue welcomed one to a world in miniature. Every shelf, nook and cranny filled with dozens of sailing boats in glass containers – bottles of all shapes and sizes (including a 5-gallon flagon), light bulbs, and even pharmaceutical glassware. Ships in bottles, modelled on historical and imagined vessels. A space primed to set a kid’s imagination free. He once showed me how he got these impossibly large models through the neck of a bottle, but he told me to keep it secret so there you have it.

One of my grandfather's model ships - a 3-masted barque — *One of my grandfather’s model ships – a 3-masted barque*

Models are descriptions of complex worlds, at scales that engulf the entire universe to the smallest atomic particle. Model descriptions are written in many different languages: discursive, mathematical-numerical, physical (the kind you can touch), conceptual-theoretical, and imaginary. We use models in all spheres of activity – politics, economics, as social organization, philosophy, and science.

Scientific models, like theories and hypotheses, are embedded in our daily discourse. As a sedimentologist, stratigrapher, general basin analyst, hydrogeologist, and sometime geochemist, I am surrounded by models that inform me about lithofacies, stratigraphic sequencing, the dynamics of basin subsidence, sediment provenance, the consequences of evolution, volcanic eruptions, and chemical equilibria. Sometimes these models are explicitly expressed in my observations and interpretations; more often they are implicit, or embedded, unseen in my cogitation of Earth science problems. Models guide me in my observations, but they also remind me to think outside the box, to look for the unusual, to question the boundaries that all models impose, and where necessary modify or replace them with new versions.

Models as representations

I’ve borrowed this heading from Frigg et al., (2020; Open access). As these authors comment, there are models for just about everything in science – “Probing models, phenomenological models, computational models, developmental models, explanatory models, impoverished models, testing models, idealized models, theoretical models, scale models, heuristic models, caricature models, exploratory models, didactic models, fantasy models, minimal models, toy models, imaginary models, mathematical models, mechanistic models, substitute models, iconic models, formal models, analogue models, instrumental models…” (Frigg et al., 2020, page 1). Most models in science, particularly the Earth sciences, are representational; they represent things, processes, and concepts. Familiar examples in science include the billiard ball model of Newtonian action-reaction (that might also double as a model for frictional losses and conservation of energy); this model is touchable – it can be observed directly. Or the iconic Bohr Model of the atom (1913) where Bohr’s theory envisages a central nucleus surrounded by electrons having orbital diameters dependent on their energy levels, analogous to the solar system. In a sense, we can also touch this model via direct observation of planetary motions around the sun. Schrödinger’s cat on the other hand is the quintessential thought experiment that is neither experimentally possible nor observable. But it does allow us to glimpse the consequences of quantum mechanics and the problem of quantum uncertainty.

Modeling in the sedimentological and stratigraphical disciplines probably began in earnest in the mid-20^th C, although the products of enlightened minds like Leonardo da Vinci’s experiments, sketches, and notes on hydraulics of channel flow tells us that inquisitive individuals have been cogitating about representation of the physical world for centuries past. And not just in the geological realm. The Renaissance and Enlightenment surge of interest in Armillary spheres as models of a geocentric universe, graced the living rooms and libraries of many well-heeled Europeans, and no doubt caused at least a few to ponder the similarities and differences between model and their night skies (and keeping their ponders to themselves for fear of conflagration).

Sedimentological and stratigraphical modeling covers the gamut of model types in Frigg et al’s., list – quantitative and qualitative; numerical and conceptual, theoretical, experimental, and analogical. Chris Paola (2000) provides an excellent reminder of the status of models at the end of the millennium. Other reviews over the next 2 decades capture the advances in general geological models (Turner and Gable, 2007), plus more focused topics like geodynamics (Shellart and Strak, 2016), rifting (Zwaan and Schreurs, 2022), orogenic wedges (Graveleau et al., 2012), and numerical modelling of sedimentary systems (Burgess, 2012; Soto, 2023).

And central to my own work, lithofacies models are fundamentally conceptual. They describe and organize data and observations into coherent structures that paint pictures of the relationships among strata, the environmental conditions that force lithological, biological, and chemical associations, and their spatial-temporal relationships. Lithofacies models are commonly expressed in written language, as 2D and 3D diagrams, time-series animations, and numerical functions. Lithofacies models are not ‘touchable’ in the normal sense of the word (unless we create scale models), but they illustrate nicely the property that many models possess – they represent crossovers among model types, for example conceptual – analogical – mathematical.

Models and analogies

The concept of analogy is intrinsic to representation in models. In very general terms, an analogy is the correspondence, similarity, likeness, or comparison of one thing to another. Analogies are NOT exact copies of the phenomena in question. Analogies can be observable, theoretical, or conceptual. In Earth science we use analogy in nearly all our deliberations concerning past events or processes – we cannot observe these events directly, but we can propose suitable analogues to help explain the geological past. For example, the commonly used expression ‘rock record’ is itself a linguistic analogy to human histories. The maxim ‘the present is the key to the past‘ gives us permission to pursue analogy to explain the rock record. The phrase was coined by Charles Lyell in his 1830-1833 Principles of Geology, based on earlier statements by James Hutton (1788) who proposed that “all past changes on the globe had been brought about by the slow agency of existing causes.” (Lyell, 1837, Volume 1, p. 92).

Thus, a modern beach becomes a realistic and useful analogue for ancient beaches; our observations of recent pyroclastic density currents permit us to model the rheology and dynamics of ancient pyroclastic flows; the organization of microbial mats and laminates in modern sabkhas and saline lakes gives us useful analogues for ancient stromatolites. Analogies like these are direct and easy to envisage. However, there are ancient geological phenomena that defy the application of obvious or direct analogy.

In some cases, the appropriate analogies for the rock record can prove difficult to establish. A good example is banded iron formations (BIF) that were a hallmark of many Proterozoic and Archean sedimentary basins – there are no modern environments that even come close to what we think the BIFs represented. In this case, possible analogues need to account for:

Ocean water masses that were saturated or supersaturated with respect to iron (II).
Waters that were saturated with respect to silica and conducive to chert precipitation.
Widespread anoxia to account for the abundance of reduced Fe(II) – Fe²⁺ oxidizes rapidly at even low oxygen concentrations (modern oceans are depleted in soluble iron).
Conditions where Fe (III) can precipitate (as hematite) but prevent the oxidation of Fe (II).
Application of these conditions to entire basins.

There is no single, all-encompassing analogy that can be applied to BIF models. We are forced to look at several possible candidates that account for different components of the model – some of the candidate analogues will seem reasonable, some may seem a bit of a stretch because they appear to be unrelated to the problem at hand. But whichever analogies are chosen, they must allow us to extend our thinking about the central problem – how did BIFs form?

For example, consider the problem associated with chert deposition. Modern, deep-sea siliceous oozes are dominated by radiolaria and diatoms which were not present during BIF formation. The physical conditions for ooze deposition are certainly compatible with BIF formation (low-energy, suspension-dominated deposition), but the biological components are not. Thus, we either reject this analogy completely or modify it by, for example, invoking the participation of Precambrian microbes. There is evidence for cyanobacterial polymerisation of silica in modern geothermal hot springs (e.g., Yee et al., 2013). Although there is no evidence for geothermal conditions in the BIFs, microbe-mediated silica precipitation might have been possible in seawater saturated with respect to silica and where cyanobacteria were abundant. Therefore, a reasonable analogue for BIF cherts might include elements of both the ooze and hot springs examples of silica precipitation.

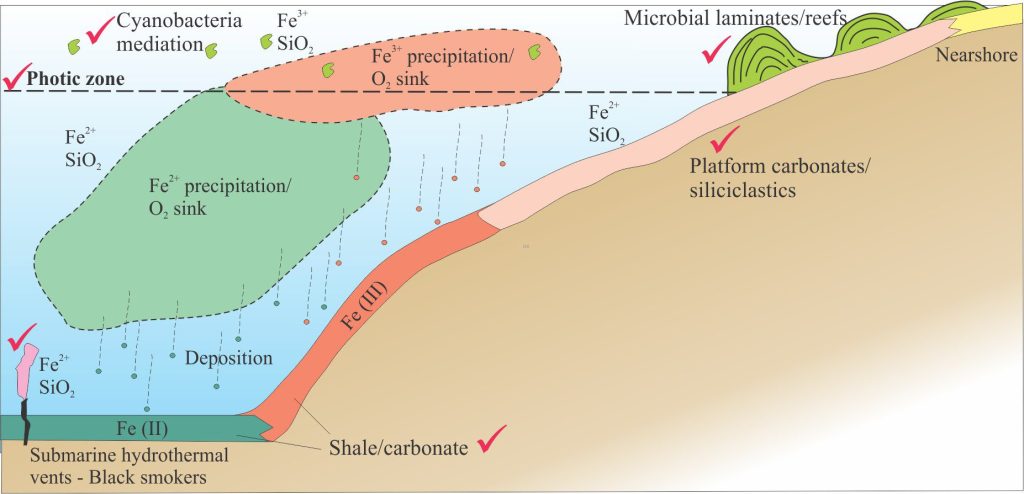
A model of BIF formation presented by Konhauser et al., (2017) and described briefly in the text, modified here to include platform and nearshore microbial biotas, plus a few extra labels. The red ticks indicate reasonable modern (and/or Phanerozoic) analogues for different components of the model.

Similar arguments apply to the precipitation of iron. One model reviewed by Konhauser et al., (2017), places the precipitation of Fe (III) in the photic zone of Precambrian ocean water- masses, where photosynthetic microbes (principally cyanobacteria) produced dissolved molecular oxygen; precipitated Fe (III) oxides then sink to the sea floor. Fe (II) oxides precipitated in more anoxic bottom waters beneath the photic zone. In this scenario, dissolved Fe (II) and Fe (III) acted as sinks for oxygen. In addition to the BIF requirements noted above, this model uses multiple analogues that describe:

The geochemical stratification of ocean waters.
The photic zone.
Microbes capable of mediating or promoting iron precipitation.

All three conditions are reasonably satisfied by modern analogues.

Models and theories

Are models also theories? From a philosophical perspective the answer seems convoluted: on one hand, models are considered dependent on theories, and on the other independent (Frigg et al., op cit.; Sterrett, 2015). Some describe theories as collections of models. The all-encompassing plate tectonic theory can be thought of as a rational collection of models, each describing a part of the general theory. For example, there are models of seafloor spreading, lithospheric subduction, rifting and transform deformation, plus a range of models that describe the kinds of sedimentary basins that form at different plate boundaries.

In this section I take the philosophically lazy approach and consider only representational models, because most models in science are of this type. Most models in Earth science are not theories in themselves, but they do contain embedded theories and laws, and in many cases other models. Inclusion of these cognitive structures may be stated explicitly or assumed. For example, in fluid mechanics, if we use Froude numbers in our deliberations then we employ the gravitational constant ‘g’ and in consequence, Newtonian theory of gravitational and inertial forces. In this case the embedded theory is written in mathematical language.

In the two examples that follow, I have listed a few of the theoretical structures that are the foundations of the models (the lists are not exhaustive!):

Foreland basin models:

At its most basic, it is a consequence of plate tectonic theory although this is commonly unstated.
Laws of gravity and thermodynamics are always assumed, and commonly stated in numerical functions.
Hooke’s Law that describes the elastic response of the lithosphere to external loads.
Models that use (analogue) elastic beams to represent the lithosphere.
Airy or Pratt isostasy
Models of the geotherm and the theory of heat transfer.
Theories and models of viscosity.
Models of lithosphere rheology.
Theories and models of stress and strain partitioning, applicable to deformation in the thrust belt, but also to fluid flow and compaction during sediment burial.
Theories and models that relate to different modes of sediment dispersal and deposition.

Depositional models of detrital sediment:

Theories and models of sediment dispersal; Ficks Law of diffusion might be applied here (e.g., Paola et al., 1992).
Theories of cohesion and friction, in the context of bedload transport of sediment.
Stokes settling velocities, Reynold’s theory that separates turbulent from laminar flow, and Froude numbers that rationalise bedform and surface wave configurations. All of these are included in any numerical and analogue modeling of sediment transport and fluid flow.
The theory of viscosity.
Boundary layer models.
Laws of gravity and thermodynamics (e.g., the conservation of energy) are always assumed, and commonly stated in numerical functions.
Facies models.

Models as predictors and pigeon holes

An important consequence of a model is that it should predict other and new phenomena. From a philosophical perspective, models may be structured according to the rules of deductive logic, but their import lies in their inductive and creative possibilities. A recent example of momentous import is the discovery of interstellar gravity waves, predicted by Relativity Theory but not measured until 2015, a century after Einstein’s prediction. The measurements were possible because of technological advances in space exploration and data analysis. Gravity waves can now be incorporated as empirically verified elements of revamped models of black hole collisions, pulsars, and other stellar interactions.

Back on Earth, one of the earliest facies models was J.R.L. Allen’s fluvial point-bar model (1965). The model provided sedimentologists with a new way to look at fluvial rocks and consequently there was a flurry of publications doing just that, many reinterpreting older explanations of fossil fluvial systems. Allen’s model applied to meandering channel systems (high sinuosity channels). The model showed the progression from channel thalweg to flood plain via sedimentation across an accreting point-bar. It was adopted enthusiastically, so much so that in some cases, even when parts of the model were not present in the actual rocks, the interpretations still insisted on high sinuosity channel point bars – in other words, forcing the rocks into some preconceived idea, an intellectual process commonly referred to as pigeon-holing.

An example of a fluvial point-bar that is reasonably consistent with a J.R.L.Allen’s 1965 model – reasonable in the sense that it contains most of the ingredients specified by the model. This example is from the Cretaceous Dunvegan Formation, northern Alberta.

Fortunately, common sense did respond to what geomorphologists had known for decades, that high-sinuosity river channels are one part in a spectrum of channel geometries and morphologies, and that a one-size model for ancient fluvial systems does not fit all. Consequently, after 6 decades of learning since Allen’s seminal publication, sedimentologists have developed multiple models for modern and ancient fluvial systems that recognise their inherent variability in time and space.

Pigeon holing is a real and present danger when applied to models. Models might be thought of as a convenience, something to trot out to reinforce our ideas, our biases. Forcing data into some preconceived model does not advance science, but it does underpin intellectual laziness. Models and the processes of modeling have immense value in science, but they should never be static. A rational model that is changed or even discarded because new information renders it no longer fit-for-purpose, does not mean the earlier version was ill conceived, but that it has successfully advocated for advancement.