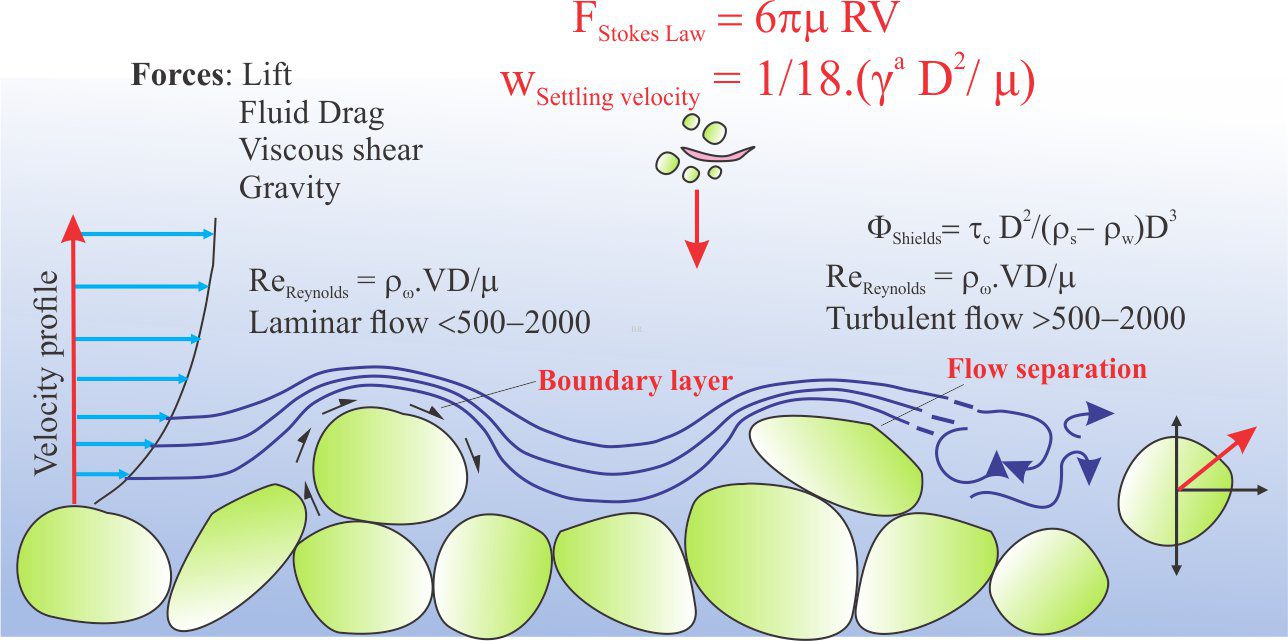
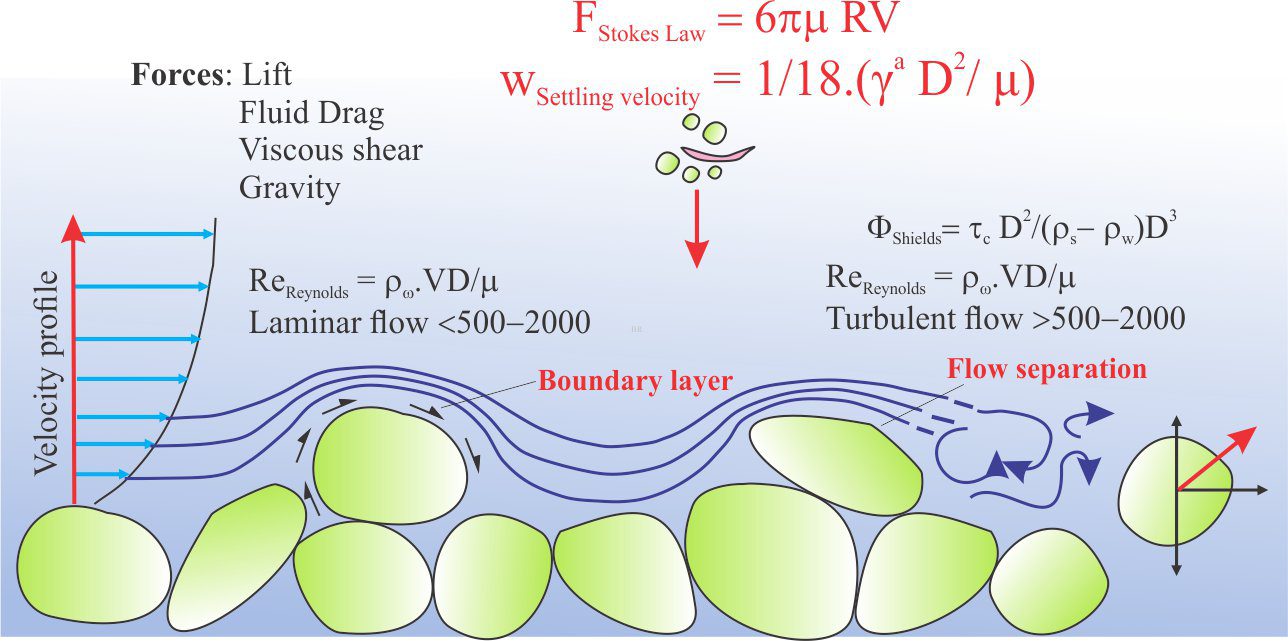
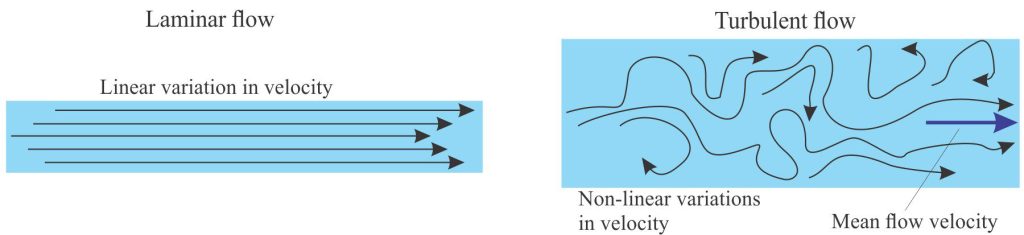
19th century experiments that helped quantify the nature of fluid flow, surface waves, and bedforms.
It all depends on inertia, like the reluctance to get out of bed on a cold winter’s morning. But rather than feeling guilty, acknowledge that by sleeping in you are adhering to the mechanical Laws that prevent the universe from collapsing – the inertial forces that keep planets in orbit around their suns, and suns in motion through their galaxies.
Inertia is loosely defined as a force that resists the change in motion of a body; here motion refers to a vector that describes velocity and direction, and ‘body’ refers to pretty well anything composed of matter, including a body of fluid. The term was coined by astronomer Johannes Kepler (17th century); his erstwhile colleague Galileo demonstrated its qualities by experimenting with balls rolling along sloping surfaces.
However, it was Isaac Newton who codified the properties of inertia in his three Laws of Motion – apparently Newton credits Galileo with the discovery. The 1st Law, also called the Law of Inertia, states that the motion of a body will not change unless an external force acts on it (i.e., to accelerate, decelerate, or change its direction). The 2nd Law quantifies the relationship between an external force F, mass (m) and acceleration (a) as F = ma. And the 3rd Law states that when an external force is applied, there will be an equal and opposite force that resists the change in motion, i.e., an inertial force – also called the Action-Reaction Law.
Inertial forces depend on the mass of a body – the larger the mass, the greater the force. In fact, the concept of mass itself is based on inertia.
Inertia and fluid flow
Inertial forces are central to the quantification of fluid mechanics. We have William Froude (1810-1879) and Osborne Reynolds (1842-1912) to thank for their eponymous numbers (Froude number and Reynolds number) that describe the characteristic states of flow. And because these numbers are dimensionless, they allow experiments with models (e.g., wind tunnels, sediment flumes) that can be scaled to real-world fluid flow phenomena. Scaling can be applied to almost anything related to fluid flow – from the motion of a boat through water, to quantifying the formation of sediment bedforms or sediment gravity flows from small-scale sediment flume experiments. The importance of Froude and Reynolds numbers cannot be overstated.
Froude number
Froude’s influential paper of 1861 was published by the Institute of Naval Architects (PDF available). Froude had surmised that, to predict the behaviour of a ship moving through water, he would need to experiment with much smaller versions of ships, or models, that could be scaled to the behaviour of much larger vessels. Thus, Froude’s number was derived from experiments with model boats, a few metres long.
The number expresses the characteristics of flow, including surface waves and bedforms, as the ratio between inertial forces and gravitational forces:
Fr = V/√(g.D)
Where V is bulk flow velocity (having dimensional units L.T-1) that reflects the dominant effect of inertia on surface flows, and the component √(g.D) where g is the gravitational constant (units of L.T-2), and D is water depth (units of L). The denominator represents the speed of a surface gravity wave relative to the bulk flow velocity (√(g.D) simplifies to units of velocity). Whether the surface wave is faster, slower or the same speed as the bulk flow will depend on its resistance to move, or its inertia. Fr is dimensionless.
The numerical value of Fr is used to define three conditions of flow. If Fr = 1 (numerator = denominator), then any surface wave will remain stationary – it will not move upstream or downstream. This condition occurs when both the velocities and water depth are at critical values. Not surprisingly, this condition is called critical flow. A common manifestation of critical flow is the formation of stationary waves (or standing waves) above and usually in phase with antidune bedforms (i.e., upper flow regime).
When Fr < 1, inertial forces dominate, and the result is a subcritical condition – tranquil flow. This corresponds to lower flow regime bedforms such as ripples and larger dune structures.
When Fr > 1, gravitational forces dominate resulting in supercritical flow conditions. The corresponding stream flow surface conditions manifest as an acceleration of flow such that stationary waves break upstream (chutes – upper flow regime), commonly followed by a rapid decrease in flow and formation of a hydraulic jump where Fr < 1 (chute and pool conditions). A hydraulic jump is the region of turbulence that represents the transition from supercritical (laminar) flow to tranquil flow – as shown in the kitchen sink example below. Supercritical flow is also common in pyroclastic density currents.

The complexity of flow transitions in a small natural system is shown in this video clip of supercritical and subcritical (tranquil) domains in a small, shallow stream. The standing waves (left) represent critical conditions where the speed of the waves matches the stream flow velocity. Supercritical conditions downstream produce chutes. Downstream migrating ripples in the foreground indicate subcritical flow.
Reynolds number
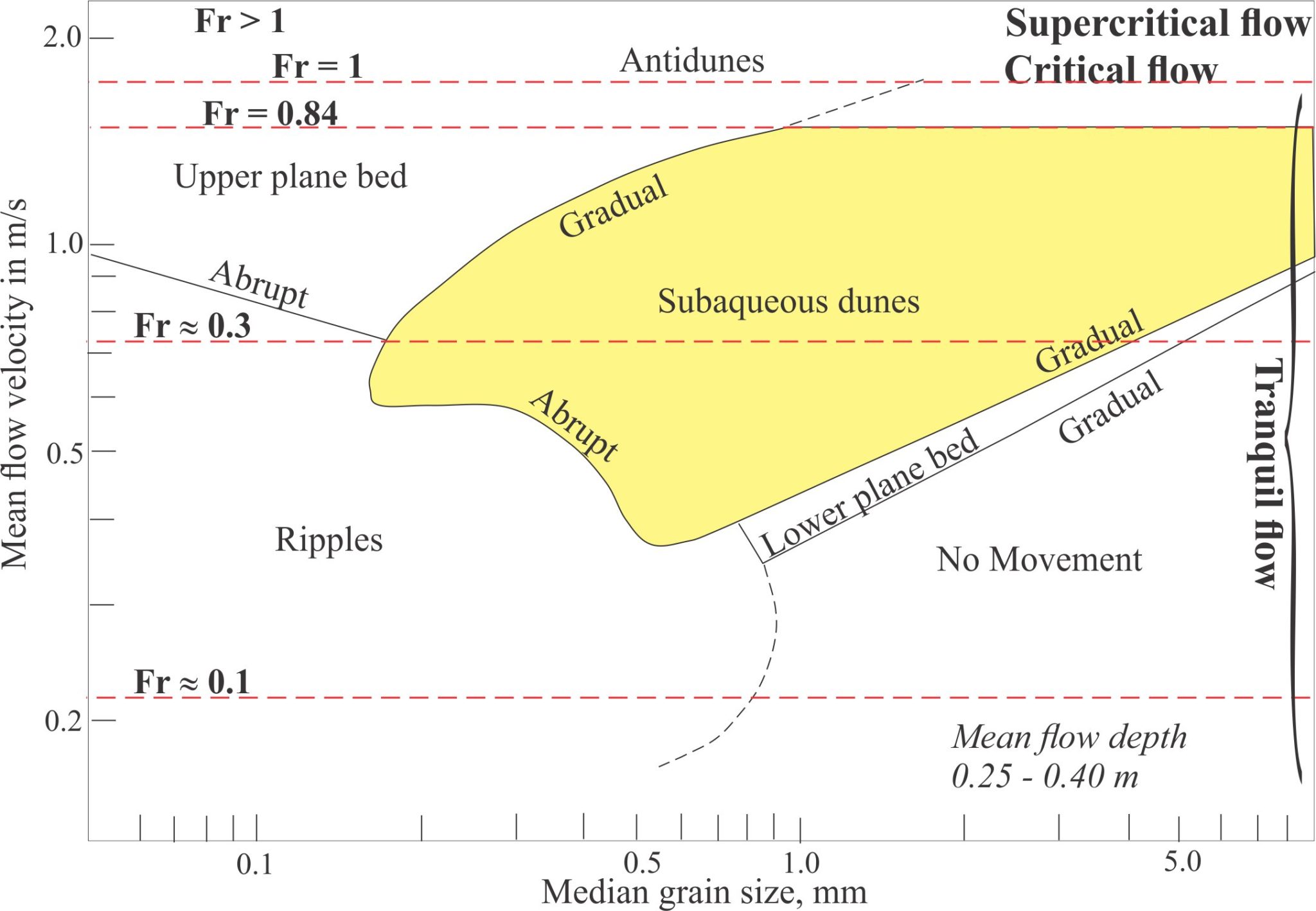
Unlike Froude who was more concerned with the surface configurations of a flowing medium, Reynolds experiments in glass pipes were concerned with the bulk structure of flow, in particular the transition from laminar to turbulent flow (Reynolds, 1883, PDF available). To picture this, think of a flowing fluid as a set of flow lines. In laminar flow, the flow lines are parallel, or approximately so, and relatively straight. The flow velocity will be the same across each flow line. By contrast, turbulence is described by flow lines that constantly change direction and velocity. In a flowing stream this is manifested as eddies, boils, and breaking waves. In sedimentary systems, turbulence is an erosive process, and an important mechanism for maintenance of sediment suspension through water columns and in sediment gravity flows.
The video below shows the abrupt transition from laminar flow in the slightly sinuous trail of smoke, to turbulent flow above.
To understand the nature of the laminar-turbulent flow transition, Reynolds considered four variables:
- Fluid density ρ (units of M.L-3).
- Fluid viscosity (μ) that measures the resistance to shear and is strongly temperature-dependent. μ has units of M.(L.T)-1
- Mean velocity of flow V, that reflects shear rate and inertia forces (units of L.T-1), and
- Tube diameter D that influences the degree of turbulence (units of L).
Reynold’s number is written as:
Re = ρVD/μ
that expresses the ratio of inertial (resistance) forces to viscous (resistance) forces. Re is dimensionless.
In his glass tube experiments, Reynolds systematically varied μ, V, and D (μ was varied by heating the water). For each combination he discovered that the transition from laminar to turbulent flow in water was abrupt, and consistently had Re values of about 12000. Reversing the experiment gave values of about 2000 for the transition from turbulent to laminar flow.
Re can be used to determine the kind of flow in large and small fluid systems. As a general rule:
- Re values <2000 indicate laminar flow,
- Re >4000 turbulent flow, and
- the region in between these two extremes reflects transitional flow.
Flow in most open-surface geological and geomorphic systems tends to be turbulent, with familiar examples including channelized flow (river, tidal and submarine channels) and more open flow across broad expanses such as continental shelves. It also includes volcaniclastic systems like pyroclastic flows and surges. Experimental flow in flumes produces a variety of bedforms at Re values that range from about 4000 to >100,000.
Laminar flow at low velocities is probably responsible for deposition of lower flow-regime plane beds; Allen (1992) has suggested that laminar flow at higher velocities may be restricted to thin sheet floods. Fluids having high viscosity, such as glacial ice and lava, commonly exhibit laminar flow. The Re value in microscopic rock-fluid systems, such as intercrystal boundaries in diagenetic environments, will also be low because fluid viscosity will dominate in such confined spaces.
Comparing Froude and Reynolds numbers
Froude numbers express a relationship between the free-surface of a flow and the various waves and ruffles that form there, and bedforms at the sediment-water interface. Reynolds numbers deal to the bulk characteristics of flow – whether it has laminar or turbulent structure.
The numbers Fr and Re are like chalk and cheese – they are not comparable. Both are dimensionless ratios, but that’s where the similarity ends. Both functions depend on inertial forces (the resistance to do anything), but for Fr the inertial component is in the denominator, and for Re in the numerator. Thus, if inertial forces become dominant, the numerical value of Fr decreases and that for Re increases.
Both numbers have application well beyond the relatively narrow field of sedimentology. Both are used extensively in scaled models – Fr for elucidating the efficacy of movement through a fluid – boats through water, airplanes through air. Re is used extensively to describe fluid flow in biological systems.
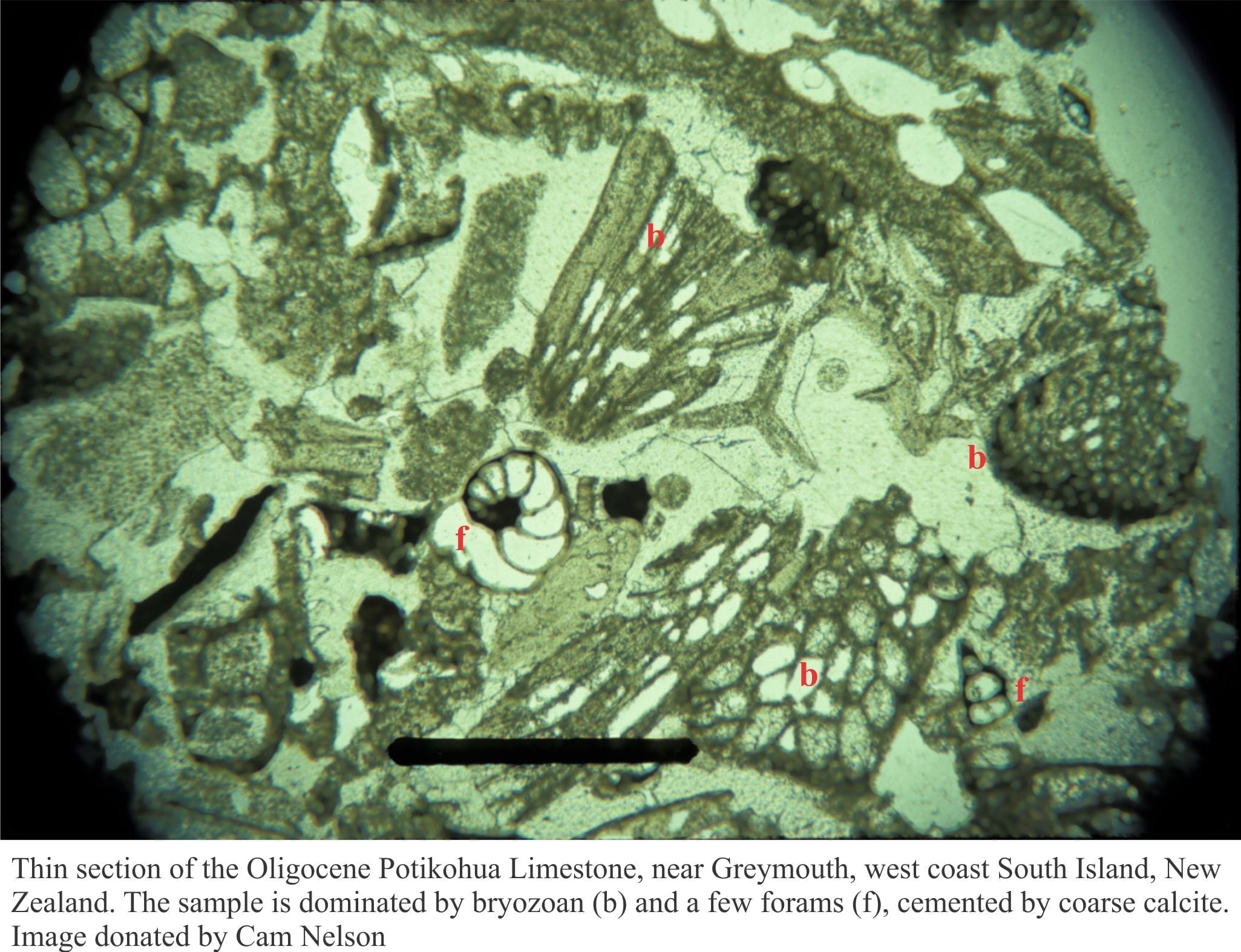
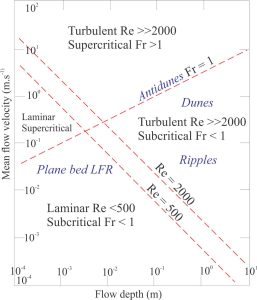
Allen (1992) has given sedimentologists a diagram that generalizes the relationship between Fr and Re in terms of mean flow velocity and flow depth. The boundaries of the 4 domains correspond to critical flow transitions; subcritical (tranquil) to supercritical for Fr, and laminar to turbulent for Re. I have added the most common bedforms to these domains.
Literature
There are many publications on this topic, but I highly recommend two publications that provide greater detail of theory and practice on this and other topics in fluid flow and sedimentation:
John Southard’s excellent (open access), online Introduction to Fluid Motion and Sediment Transport.
J.R.L. Allen 1992 (and later editions) Principles of Physical Sedimentology (that no sedimentologist should be without).
Other posts in this series
Identifying paleocurrent indicators
Measuring and representing paleocurrents
Crossbedding – some common terminology
Sediment transport: Bedload and suspension load
The hydraulics of sedimentation: Flow regime