
Physical experiments on natural systems commonly employ scaled models. A guiding principle of model design is to maintain similarity between the model and real world in terms of their geometry, kinematic behaviour, and dynamic behaviour. Similarity is achieved by scaling the appropriate variables that operate in both the model and natural system. Models that are scaled correctly allow us to predict and quantify the behaviour of natural systems that are otherwise too large or too difficult to observe and measure directly. Sediment gravity flows fall into this category – monitoring their initiation and progress is physically difficult, not to mention hazardous.
Scaling laws and scaling factors
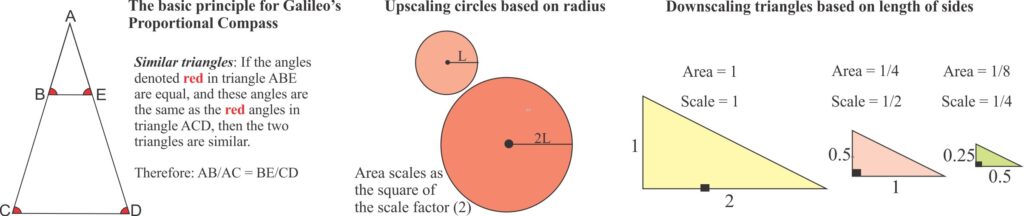
Scaling laws are statements of proportionality associated with the scaling of an object or process. Galileo was one of the first to consider these laws, using similar triangles as the basis for constructing his proportional compass. The laws are expressed mathematically as power functions of the form:
y ∝ xa, and y = bxa where x is a measured quantity, a is the scaling exponent, and b is a proportionality constant. x, y, and b are positive numbers; the exponent can be positive, negative, or zero. For example, the scaling law for volume is the cube of a measured length.
The scale factor (designated λ) describes in numerical terms how much the size of an object is increased (e.g., from model to prototype) or decreased for a particular quantity or measurable attribute of that object, such as length. For example, if we upscale a circle of radius 2L units to 4L units the length ratio is 2/1 (scale factor = 2), then the length of the diameter and perimeter are doubled. However, the circle area increases from 12.57 L2 to 50.27 L2, corresponding to the square of the length ratio. In other words, the scale factor for length is λ1, and for area it is the square of the scale factor for length, or λ2 where the exponents correspond to the scaling law exponent.
Note that descriptive phrases for scaling such as “doubling in size” are misleading unless the context is clearly stated – are you doubling length, area, or volume?
Spherical or cubic cows
Chris Paola in 2011 posed a question about the value of our single-minded pursuit for modeling simplicity – are spherical cows really necessary? Do they advance our understanding of process? The fence-sitting answer (perhaps the fence that controls the cows) is yes and no. No because a reliance on similitude is not necessarily the path to creative thinking and insight, and yes because we can upscale the model results to the real world, where variables like turbidity current runout distances can be quantified. These are useful results even if they aren’t particularly creative.
So, what are spherical cows? [the analogy or metaphor is commonly attributed to G. Harte, 1985 in text “Consider a Spherical Cow: A Course in Environmental Problem Solving” but it probably was stated using different critters in the early 1970s. PDF available on Researchgate].
The easiest way to model cows (for whatever arcane reason) is to simplify their geometry such that we maintain the similarity of all the variables we wish to test, for example cubic or spherical cows. If a cubic cow has unit side lengths (L) then the area of a side is L2 and the total area is 6L. The volume is L3 = 1.
If we double the length to 2 units (i.e. a scale factor of 2), then L = 2, L2 = 4, and L3 = 8. However, if we scale down the length by half, L = 0.5, L2 = 0.25, and L3 = 0.125; in other words, smaller cows have proportionately larger surface areas than larger cows. If we calculate the surface area and volume for spherical cows with radius Ls, we find the same proportionality relationships hold. Thus, our general scaling laws for length, area and volume are L1, L2, and L3, and the scaling factors are λ1, λ 2, and λ 3 respectively, regardless of model shape.
In considering the scaling for mass, we know that density is the same for both model types, and that density does not vary with size. Thus, density in the real world is the same as that in our model and therefore scales as 1 (λ0). However, mass = volume (L3) times density which means that the scale factor for mass = λ3. λ0 – in other words, mass scales as cube of the scale factor for length (λ3). This applies to both cow models.
What about scaling dynamic variables? Our cubic cow will exert pressure on the lab floor. Pressure (stress) P is force per unit area, and force F, according to Newton’s 2nd Law is F = m.a (mass times acceleration). In this case acceleration is the gravitational constant ‘g’ that applies to any object, no matter its size and shape – thus g scales as λ 0 (i.e. 1 times its value at Earth’s surface). Therefore, the force F exerted by gravity scales as L3.L0, force scales as λ 3; this means that larger objects experience forces greater by a power of three. Thus, if our cows were gigantic, their bone size and strength would also need to increase proportionally otherwise they would collapse under their own weight (we also see this when comparing elephants and mice). The scaling law for force can now be applied to pressure or stress in terms of length scales as L3.L-2, or a scale factor of λ 1.
Kinematic analysis deals with the rates at which things take place; common examples are flow velocity, acceleration, and strain rate all of which contain a time term. The easiest way to determine a scale law for time is to rearrange the expression for acceleration – g = m.s-2 (L.T-2). Given that gravitation acceleration scales to λ 0, we can rewrite the expression as T = √L. Thus, the scale factor for time is λ0.5. Likewise, the scale factor for velocity is also λ0.5. This means, for example that if a natural turbidity current flows at 1 m/s, the model version needs to downscale to 10 cm/s to maintain similarity.
The disproportionate influence of variables
When a variable is scaled, we are expressing a difference in magnitude between model and natural system. One of the interesting facets of scaling is that, whereas individual variables differ only in magnitude between model and real systems, the relative importance among different variables can change. We have already noted this for length scales where small particles have proportionally larger surface areas for a particular volume than larger objects (this is an important phenomenon in diagenesis where the surface free energy of small particles like clays can contribute to their reactivity). We also see this kind of disproportionate affect in dynamic variables like force for example, fluid flow through a large diameter pipe occurs unobstructed, but flow of the same fluid through a very thin tube (same viscosity, temperature) is impeded by surface tension forces.
Froude similarity and Froude scaling
The Froude similarity is often applied in experimental fluid dynamics. The Froude number (F) is usually written as F = U/√g.h where U is velocity, h is a characteristic length such as depth, and g is the gravitational constant. Mathematically F expresses the relationship between flow velocity and length (depth); conceptually it is the ratio of inertial to gravitational forces such that at high flow velocities inertial forces suppress gravitational forces. In the context of experimental turbidity currents, F:
- Is dimensionless which means it is independent of the size of the system under investigation.
- F determines the flow regime – subcritical or supercritical flow, and
- F determines degree of density current mixing with the ambient fluid at the flow head; too much mixing at high Froude numbers (>1) will rapidly dilute the flow (Middleton, 1966; Middleton, 1993 Sediment Deposition from Turbidity Currents).
Thus, Froude similarity between model and prototype is essential if we want to compare and upscale or downscale our experiments to real world phenomena. This usually means we need to tweak variables such as grain size, flow density or depositional slope in the experiment design so that that we can demonstrate similarity of all variables of interest between model and prototype. Scale factors commonly used in hydrodynamic experiments, including those with turbidity currents, are listed below.
Variable Units Dimensions Scale factor
Acceleration m.s-2 LT-2 λ0
Area m2. L2 λ2
Density kg/m3 ML-3 λ0
Force N MLT-2 λ3
Length m L λ1
Mass kg/m3 ML-3 λ3
Pressure N/m2 ML-1T-2 λ1
Speed m/s LT-1 λ0.5
Time s T λ0.5
Densiometric Froude scaling
Bottom-hugging turbidity currents operate by virtue of gravitational forces acting on suspensions of sediment and water over a sloping substrate. The bulk density of these flows can be significantly greater than the ambient fluid through which they move. Thus, experimental flows require a correction to account for this density difference – the Densiometric Froude number:
Fdens = U/√g’h where g’ is the density-corrected, or reduced gravitational constant that is calculated from g’ = g (ρ1−ρ2/ρ1) where ρ1 is the density of the flow and ρ2 is the density of the ambient fluid; h is the flow thickness, commonly taken at the flow head – h can also be used for a characteristic grain diameter. The conditions for similarity and scaling applied to Densiometric Froude scaling are the same as those for standard Froude scaling.
Other posts in the turbidity current series
Experiments with turbidity currents – some historical context

















