Mineralogy of evaporites: saline lake brines

The evolution of brines that produce saline lake evaporites.

This is part of the How To…series  on evaporites

Seawater is generally considered to be isochemical because its composition varies little from sea to sea. There are some changes in saturation levels of calcite and aragonite in deep ocean waters (below their compensation depths), and salinity in basins having more restricted seawater inflow (e.g. Mediterranean Sea, Arabian Gulf), but the range of composition variation is limited. This means that evaporation of seawater follows a predictable chemical and thermodynamic path.

Not so terrestrial waters (rivers, groundwater) whose starting compositions are remarkably varied. Most natural waters contain Na in abundance plus an array of cations and anions like K⁺, Ca²⁺, Mg²⁺, Cl^–, SO₄^2-, HCO₃^–, CO₃^2-, and SiO₂. But the starting concentrations of these ions varies greatly meaning that the resulting evaporite mineralogy is also varied. Enter Lawrence Hardie and Hans Eugster whose chemical modelling in the late 1960s and 70s showed us how to make sense of this natural variability and complexity. Their publications are still cited 50 years later (a few are listed below); they are compulsory reading for any student who is interested in evaporites and geochemistry.

Hardie and Eugster (1970) calculated evaporation paths and mineral products for natural waters having different compositions at atmospheric pressure and 25^oC. The waters are assumed to be in equilibrium with CO₂ (pCO₂ is constant) – this is important for CO₃^2- and HCO₃^– and calculation of pH.  Some of the relevant calculations have been described in a previous post on carbonate geochemistry – the same principles apply to evaporites.

• Equilibrium constants for each mineral (common evaporite minerals from saline lakes are listed below),
• Ion activities and activity coefficients,
• Ion activity products (IAP),
• Degree of mineral saturation,
• Ionic strength, low values in dilute water, increasing with evaporation,
• Note that complex ion pairs are not included in the calculations.

As water evaporates, the activities of cations and anions increases. If the ion activity product equals the equilibrium constant for a mineral, then the solution has become saturated and that mineral will precipitate; at this point the IAP remains constant. The important results in this process are, using calcite as an example:

• During precipitation, both Ca²⁺ and CO₃^2- are removed from the original water in equal proportions,
• Calcite will continue to precipitate until one or both Ca²⁺ and CO₃^2- have been depleted.
• It is likely that the original concentrations of Ca²⁺ and CO₃^2- are not equal. If, in this example Ca²⁺ > CO₃^2-, then calcite will precipitate until the CO₃^2- is used up, leaving excess Ca²⁺ available for some other mineral like gypsum.
• If on the other hand Ca²⁺ < CO₃^2-, then the Ca²⁺ will be depleted first leaving none for gypsum.
• Water is continually removed during evaporation and its concentration decreases; if the process proceeds to desiccation then the concentration of water is zero.

As evaporation proceeds the model predicts which minerals are likely to precipitate and which will not, depending on the starting composition of the water. The succession of mineral precipitates defines the evaporation path for that particular water.

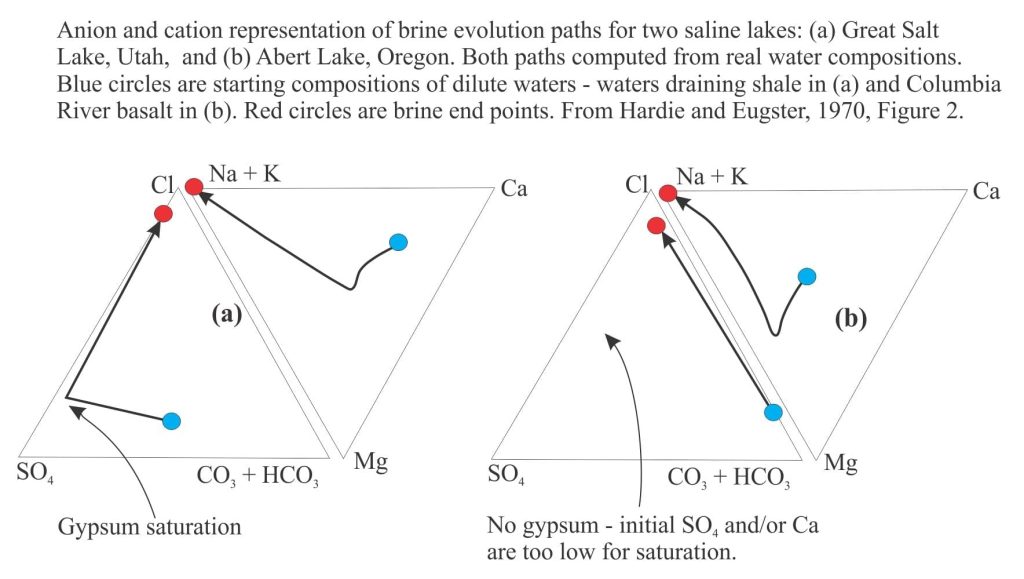
Two reasonably typical examples are shown below (from Hardie and Eugster, 1970, Figure 2). Here, the apices of each triangle plot the changes in ion concentrations as evaporation proceeds. For the example of calcite precipitation, the path moves away from the Ca and CO₃^2- – HCO₃^– apex towards the Cl apex.

Note that the evaporation paths turn abruptly at the point where precipitation depletes the relevant ions.

Example (a): Sulphate rich water that evolves to a Cl brine via precipitation of gypsum.

Example (b): Carbonate rich – sulphate poor water; no gypsum precipitates and the system evolves to a CO3–Cl brine. If calcite precipitates, the brine will likely become rich in Na and K. Halite saturation will be reached if evaporation continues.

In their model, brine evolution curves are complicated by SiO₂ and precipitation of sepiolite (illustrated in the flow-path diagrams below). Sepiolite is a hydrated Mg-silicate; its precipitation will influence the Mg path. Precipitation of sepiolite also releases H⁺ and is therefore an important part of pH buffering (along with the carbonate equilibria). As pH is lowered, CO₃^2- will decrease. Therefore, there is potential for reversal of the CO₃^2- enrichment trends.

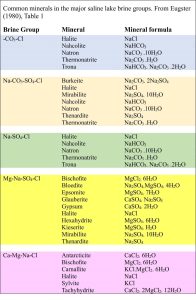
Hardie and Eugster (1970) identified 4 important groups of natural waters; Eugster and Hardie (1978) added a fifth group. Note (1) not all waters will fit neatly into one of these groups, and (2) the ions that define each group are dominant –subordinate cation and anion species will also be present:

• Na–CO₃-Cl
• Na–CO₃-SO₄–Cl (e.g. Lake Magadi, Kenya)
• Na–(Ca)–SO₄-Cl (e.g. Great Salt Lake, Utah)
• Mg–Na–(Ca)–SO₄-Cl (Poison Lake, Washington)
• Ca–Mg–Na–(K)–Cl (Bristol Dry Lake, Mohave Desert, California; Dead Sea)

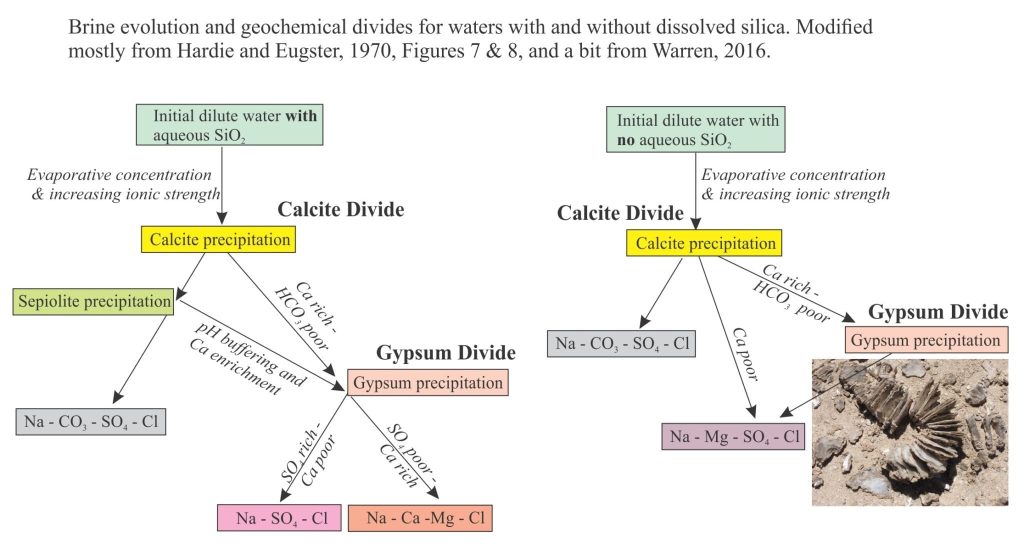
In all waters, alkali metal carbonates are the first to precipitate, particularly calcite or aragonite depending on the Mg/Ca ratio. This is a critical first stage in evaporation because it determines the subsequent precipitation sequence of minerals as Ca²⁺ and CO₃^2- are removed from solution. This is the Calcite Divide, separating waters that become HCO₃ rich or  HCO₃ poor (keep in mind that continued evaporation increases the overall ionic strength). Depending on the SO₄ concentration, excess Ca results in gypsum precipitation that, in turn, creates the next geochemical divide – the gypsum divide that determines whether the brines evolve as SO₄ rich – Ca poor, or SO₄ poor – Ca rich. One of the last minerals to precipitate is halite from Cl-rich brines.

Brine evolution is shown diagrammatically below (modified from Figures 7 & 8 in Hardie and Eugster, 1970; Warren, 2016, Fig. 2). The two pathways represent waters that include sepiolite precipitation, and those lacking significant aqueous SiO₂. For the case where sepiolite precipitates, there is an additional path towards gypsum saturation because of the pH effect on CO₃-HCO₃ (noted above), such that the brine becomes enriched in Ca.

You should also check the flow diagram in Warren (2016) Figure 2, that shows in greater detail complications such as changes in Mg/Ca ratios, variations in HCO₃, in addition to sepiolite production.

In this post, I have focused on the work of Hardie and Eugster because it has been pivotal in guiding more recent research. Of course, there have been modifications and improvements to their models, and you can access these recent advances in the literature cited below.

Links to related topics

Mineralogy of evaporites: The rise of diapirs

Mineralogy of evaporites: salt tectonics

Mineralogy of evaporites: Saline lakes

Mineralogy of evaporites: Death Valley hydrology

Mineralogy of evaporites: Marine basins

Mineralogy of carbonates; classification

Mineralogy of carbonates; carbonate factories

Mineralogy of carbonates; basic geochemistry

Mineralogy of carbonates; meteoric hydrogeology

Mineralogy of carbonates: sabkhas

References

M. Babel and B.C. Schreiber, 2014. Geochemistry of evaporites and evolution of seawater. Treatise on Geochemistry. Elsevier, p. 483-560. Deals with marine evaporites but many aspects relevant to non-marine. Encyclopedic with extensive list of references

D.M. Deocampo and B.F. Jones. 2014. Geochemistry of Saline Lakes. Treatise on Geochemistry. Elsevier, p. 437-469. Encyclopedic with extensive list of references

H.P.Eugster, 1980. Geochemistry of evaporitic lacustrine deposits. Annual Review of Earth & Planetary Sciences, v. 8, p. 35-63.

L.A. Hardie and H.P.  Eugster, 1970. The evolution of closed basin brines. Mineralogical Society of America, Special Paper v. 3, p. 273-290. 50 years old but still an iconic paper and a must-read.

J. Warren, 2016. Evaporites. In W.M. White (Ed.) Encyclopedia of Geochemistry. Springer International, p. 1-8. Concise summary of saline lake and marine brine.