Some basic geochemistry of carbonates, carbonic acid and carbon dioxide
This is part of the of How To…series… on carbonate rocks
Sedimentary carbonate petrology is concerned first and foremost with the precipitation and dissolution of mineral phases; principally calcite, aragonite and dolomite. Both processes involve chemical reactions and the two primary requirements for these reactions are:
- thermodynamics – there needs to be sufficient energy to drive the reactions, and
- an excess or deficit of dissolved mass that, for the minerals of interest, includes Ca2+(aq), Mg2+(aq), and CO32-(aq) (aq = aqueous)
All sedimentary carbonate reactions at the surface or during sediment burial take place in water: fresh water, sea water, or concentrated brines. Furthermore, the chemical composition of these fluids can evolve, for example during burial (sea water to brine), or uplift and exposure (sea water to fresh meteoric water). Such changes are commonly manifested as cement stratigraphy (e.g. high-Mg calcite overlain by low-Mg calcite), or where clasts, matrix and early cements are replaced by new generations of calcite or dolomite.
We are also interested in carbonate reactions because of the present trend towards climate change and the possibility that ocean chemistry may change; ocean acidification tops the list here. To get beyond the hyperbole, to determine whether this is a real possibility or not, we need to understand some basic chemistry. Some introductory concepts are outlined herein.
To delve deeper into the complexities of the carbonate system, have a read of the contributions cited below.
Carbonate Equilibria
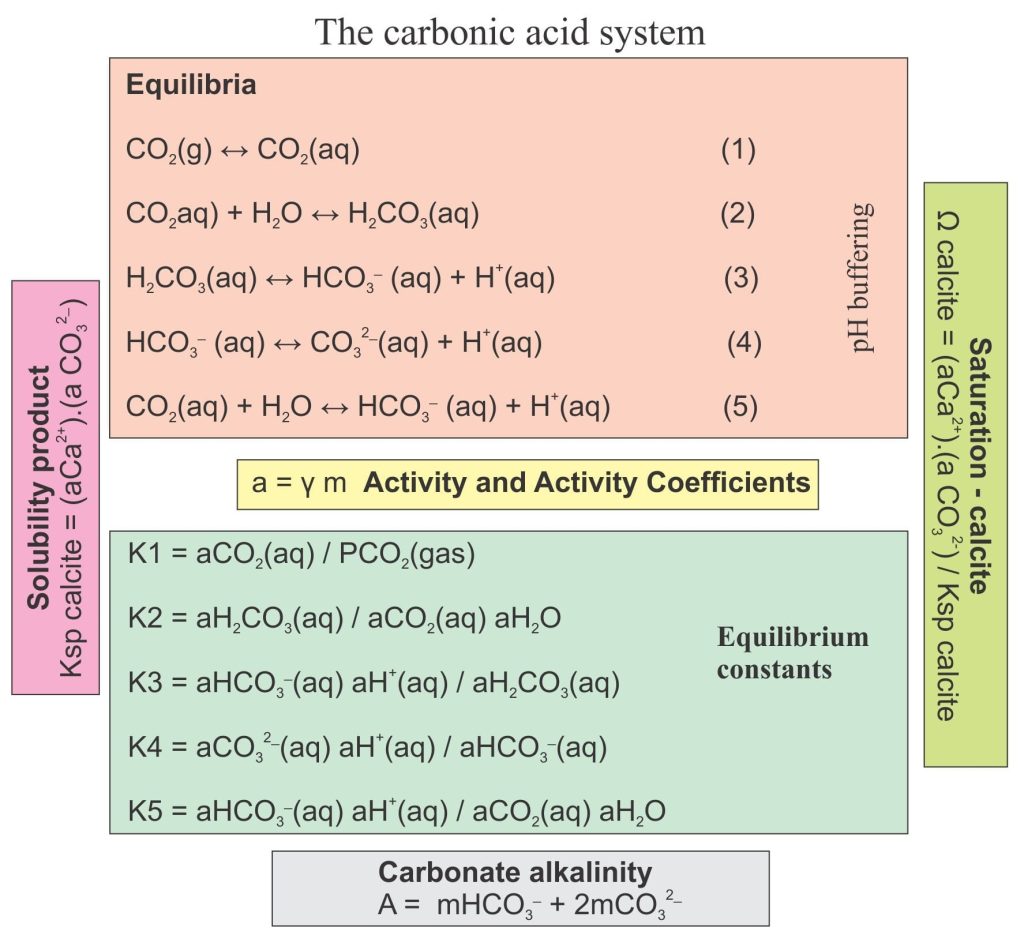
Carbonate chemistry focuses on reactions involving carbonic acid (H2CO3) and carbon dioxide (CO2). Here the most important reactions are written as equilibria. Each reaction will move left or right depending on an excess or deficiency of any ion species. So, if CO2 gas is added to the system, there will be an increase in dissolved CO2 (reaction 1) and a concomitant cascade effect in all the other reactions.
CO2(g) ↔ CO2(aq) (1)
CO2(aq) + H2O ↔ H2CO3(aq) (2)
H2CO3(aq) ↔ HCO3– (aq) + H+(aq) (3)
HCO3– (aq) ↔ CO32-(aq) + H+(aq) (4)
Morse and Mackenzie (see reference below) combine equations (2) and (3) where the H2CO3(aq) cancel:
CO2(aq) + H2O ↔ HCO3– (aq) + H+(aq) (5)
At equilibrium there is no net gain or loss of reactants (by convention, the left side of the equation) or products and no net change in energy. Note that this does not mean the system is static – even at equilibrium there are still collisions between ions (all reactions in solution involve collisions), but collisions on the left equal those on the right side of the equation.
An important point about carbonate equilibria is that they do not operate in isolation. The importance of H+ and pH buffering is a good example. If the amount of dissolved CO2(aq) is increased this does not mean that the amount of H+(aq) will increase by the same amount because some of the CO2 forms H2CO3 (aq), some HCO3– (aq), and some CO32- (aq), such that the amount of H+ added is small. In other words, the cascade of equilibria acts to buffer the system against large changes in pH. Knowledge of the carbonic acid equilibria are critical to any discussion on ocean acidification. The pH of modern sea water is 7.5 to 8.4.
The Activity of ion species
In an aqueous solution, the concentration of a species like Calcium can be measured – the value, commonly expressed as moles/liter, represents the total amount of Ca in solution. Thus, we might assume that all this Ca2+ (and CO32-) was available for a reaction like:
Ca2+(aq) + CO32-(aq) ↔ CaCO3(solid)
At this point we need to introduce the concept of reactivity, more commonly known as activity (a). Activity is sometimes referred to as the effective concentration, but this can be a bit misleading. In a solution like sea water there are many different cations and anions, all reacting to collisions of various kinds. For example, the CO32- anion may collide with cations other than Ca2+ (Na+, Mg2+, K+ and so on), such that the amount of CO32- available to react with Ca2+ is less than the measured concentration. In other words, the amount of CO32- available in real solutions depends not just on its overall concentration, but also on its environment – hence the expression effective concentration. The activity of an ion is the ratio of its concentration versus some standard concentration and is therefore dimensionless (unlike concentration). The other important difference is that activities are used in thermodynamic calculations, such as equilibrium constants. Note too that the activity of solids is usually taken as 1.
Activity coefficients
The activity of an ion species is related to its concentration by the activity coefficient (γ) for that species, by the equation:
a = γ m (6)
where a is the activity and m is concentration for the specified ion. It is a critical part of any carbonate geochemical and thermodynamic analysis. γ for a specific ion species is related to the degree of ionic interaction with other species in solution. For dilute solutions γ approaches 1 because there are few ion interactions (γ is dimensionless). Thus, the γ value for HCO3– in fresh river water averages about 0.95, but in sea water is much lower (0.57) because of ionic interactions. Therefore, the activity of HCO3– (from equation 6) is significantly higher in fresh water than in sea water even if the total concentration is the same in both.
Determining γ can be difficult – for a good summary of the different methods I suggest you check Morse and Mackenzie (referenced below).
Equilibrium constants
The reactions depend on ion concentrations, temperature and pressure. Treating them as equilibria means that we can calculate reaction constants at a specified temperature and pressure (usually 25oC and 1 bar). Equilibrium constants are the ratio of product activities (or concentrations) divided by reactant activities; they can be determined experimentally (assuming a reaction is at equilibrium) or using thermodynamic considerations (where activities must be used).
The general expression for a reaction involving ionic species in solution is:
aA + bB ↔ cC + dD
where a, b, c, and d are the stochiometric values for each ion (e.g. 2H+). We calculate an activity quotient (Q) thus:
Q = (aC)c (aD)d / (aA)a (aB)b (7)
where a is the activity (from equation 6). At equilibrium, Q is given the special name equilibrium constant (K). The carbonic acid system constants are (from 1 to 5):
K1 = aCO2(aq) / PCO2(gas)
K2 = aH2CO3(aq) / aCO2(aq) aH2O
K3 = aHCO3–(aq) aH+(aq) / aH2CO3(aq)
K4 = aCO32-(aq) aH+(aq) / aHCO3–(aq)
K5 = aHCO3–(aq) aH+(aq) / aCO2(aq) aH2O
In dilute solutions it is reasonable to use concentrations rather than activities because the activity coefficient tends towards 1. In more saline solutions, like sea water, this is not a good idea for reasons noted above.
The value of K applies to reactions at equilibrium. In real solutions we can determine if a reaction will proceed to the right or left, for example the reaction (4)
HCO3– ↔ CO32- + H+ (a necessary step to precipitation of calcite)
by using the measured activities to calculate an activity quotient (using the formulae for Q). We then compare Q with K such that:
- At equilibrium Q = K (no net change in products or reactants),
- If Q < K the reactants will convert to products – the reaction will go to the right,
- If Q > K the products will convert to reactants – reaction goes to the left.
Solubility product
We are also interested in how much a carbonate mineral will dissolve in fresh water or sea water under specified conditions of temperature and pressure. For calcite this is written as:
CaCO3(solid) ↔ Ca2+(aq) + CO32-(aq)
The equilibrium solubility product is:
Ksp = (aCa2+).(a CO32-) / (a CaCO3 solid)
The activity of the solid calcite is 1, such that the constant becomes
Ksp = (aCa2+).(a CO32-)
The solubility of calcite, aragonite and dolomite are very low, and Ksp values are often expressed as Logs. The higher the value, the lower the solubility. Typical values at 25oC and 1 bar are:
Calcite – 8.48 to 8.50
Aragonite – 8.28 to 8.34
Dolomite – 16.7
Carbonate saturation
The amount of carbonate available for precipitation in sea water is critical to nearly all marine life. If we measure the CO32- concentration in sea water and know the solubility product of calcite and aragonite at the same temperature and pressure, we can determine whether these waters are deficient or have excess dissolved CO32-. This condition is called saturation (Ω): Saturation is the ratio of the measured ion activity (or concentration) product and the standard solubility product for a mineral.
Ω calcite = (aCa2+).(a CO32-) / Ksp calcite
An excess of CO32- over Ksp (Ω >1) and sea water is supersaturated with respect to calcite (or aragonite); if sea water has less CO32- than the equilibrium solubility product (Ω <1) then it is undersaturated and calcite/aragonite will dissolve. If Ω = 1 then calcite or aragonite are at equilibrium with sea water.
Modern tropical and subtropical sea waters are supersaturated by about 4.2 times with respect to aragonite, and 6.3 times for calcite (aragonite is more soluble). The degrees of supersaturation for both minerals in polar waters is significantly less (about 1-2 times) because of higher concentrations of dissolved CO2 and slightly lower pH values (i.e. more acidic).
Alkalinity as a measure of pH buffering
Alkalinity is a measure of the amount of acid that can be added to an aqueous system without causing significant changes to the pH; also referred to as the acid neutralizing capacity. It is a useful indicator in natural waters because it is based on measured concentrations. For the carbonate system it is defined as:
Acarb = mHCO3– + 2mCO32-
In sea water, other species such as boric acid and some organic compounds will contribute to the total alkalinity. Alkalinity is an important parameter when considering pH buffering in ocean waters, paricularly waters above the thermocline because it is there that most photosynthesis and associate biotic activity takes place. Any change in pH, particularly toward the acidic end of the scale, requires massive volumes of carbon dioxide to exchange between the atmosphere and seawater.
Alkalinity is a measured quantity, as are pH, total CO2 and CO2 gas pressure. These values can be substituted into the carbonate equilibria to calculate the concentrations or activities of other ion species.
Links to other posts in this series:
Mineralogy of carbonates; skeletal grains
Mineralogy of carbonates; non-skeletal grains
Mineralogy of carbonates; lime mud
Mineralogy of carbonates; classification
Mineralogy of carbonates; carbonate factories
Mineralogy of carbonates; cements
Mineralogy of carbonates; sea floor diagenesis
Mineralogy of carbonates; deep sea diagenesis
Mineralogy of carbonates; meteoric hydrogeology
Mineralogy of carbonates; Karst
Mineralogy of carbonates; Burial diagenesis
Mineralogy of carbonates; Neomorphism
Mineralogy of carbonates; Pressure solution
Mineralogy of carbonates; Sabkhas
Some useful readings:
J.W. Morse and F.T. Mackenzie 1990. Geochemistry of sedimentary carbonates. Developments in Sedimentology 48. Elsevier, Amsterdam, 707 p.
P.A. Domenico and F.W. Schwartz, 1997. Physical and Chemical Hydrogeology, 2nd Ed. John Wiley & Sons. 506 p. This book focuses on groundwater but has an excellent section on aqueous chemistry.
M.M. Benjamin, 2002. Water Chemistry. McGraw-Hill. 668 p. This is a fairly advanced topic.
A.M. Alonso-Zarza and L.Tanner (Eds.), 2009. Carbonates in Continental Settings. V. 62. Elsevier, 336 p.