Mohr-Coulomb failure criteria

3850

*Conjugate fractures and en echelon tension gashes – indicators of brittle failure in Old Red Sandstone, Gougane Barra, County Cork, Ireland.*

Brittle deformation and Mohr-Coulomb failure

Deformation of Earth materials takes place predominantly within two rheological domains: brittle and ductile. Deformation close to the Earth’s surface is dominated by brittle failure (faults, fractures, and joints); ductile behaviour of rock become increasingly important deeper in the crust and lithosphere mantle – exceptions include the deformation of ice and salt at shallow depths. Ductile deformation depends on differential stress, material viscosity, and time, where the latter is generally couched in terms of strain rate. Brittle failure also depends on strain rate, but at the opposite end of the scale; it is also a function of rock strength.

Rock strength is a measure of the stress required to produce failure. It has the units and dimensions of stress, commonly expressed as megapascals (ML^-1T^-2). Rock strength is defined for tensile and compressional conditions – joints are mostly tensile structures whereas faults and fractures involve components of shear with dip-slip, strike-slip or oblique-slip movement along planes of failure. In general, compressive strength exceeds tensile strength within the crust.

Measurement of rock strength

The strength of any material can only be determined by experiment. For hard rock the most common tests are the uniaxial and triaxial compression tests. Triaxial tests can also be used for unconsolidated soil and sediment, but other methods like cone penetrometry are probably more useful for determining resistance to stress.

Uniaxial and triaxial tests subject a small cylinder of rock to axial normal stress (σ₁) using a piston at one end of the cylinder. In uniaxial tests the rock cylinder is unconfined such that σ₂ = σ₃ = 0). For triaxial tests, rock cylinders are enclosed in a jacket of rubber or metal that is pressurized, commonly by oil or some other fluid that surrounds the jacketed sample; in this case σ₂ = σ₃ > 0. Tests with this apparatus will usually increase the confining pressure incrementally. The piston pressure value at the point of failure corresponds to the material strength. Typical triaxial stress-strain curves are shown below.

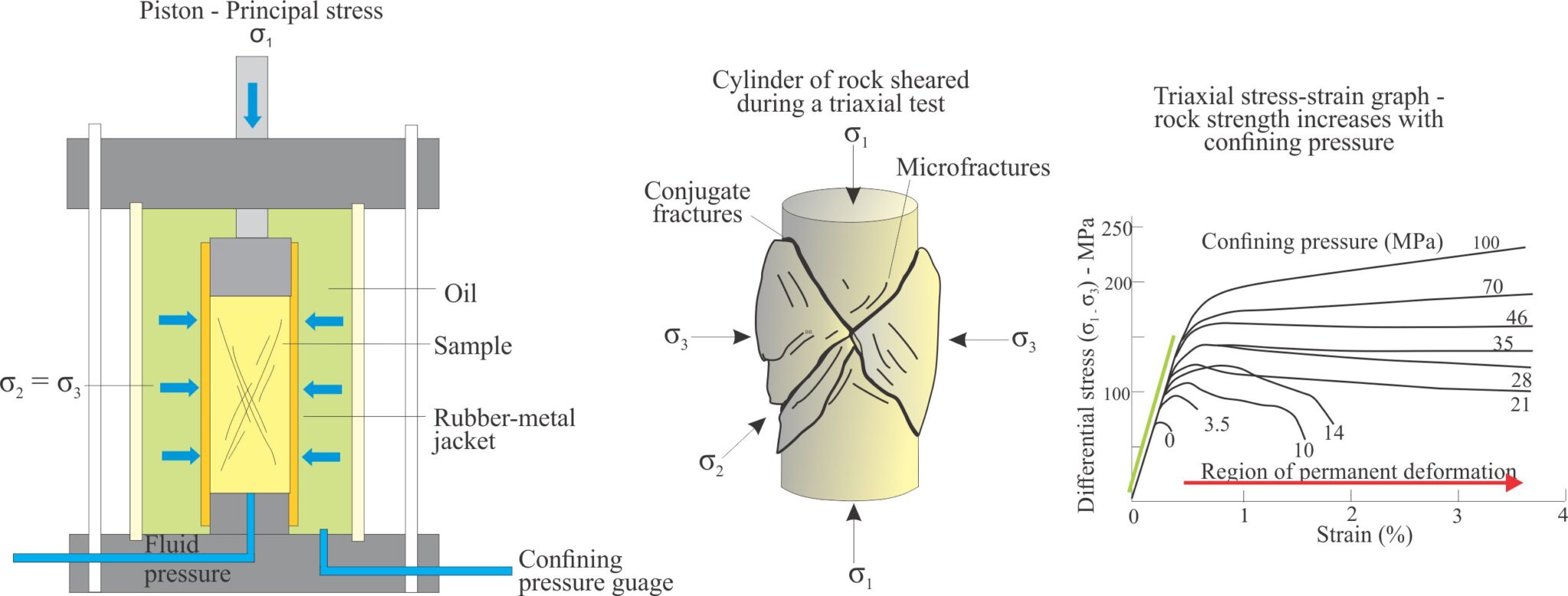
A schematic of a typical experimental set-up for triaxial tests on rock samples. Confining pressure is increased by increasing the pressure on the oil surrounding the jacketed rock cylinder (from R. Weijermars 2023, Principles of Rock Mechanics, Figure 6.11b. Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. PDF available).The example of sheared rock shows fracture planes that are highly irregular, plus subordinate microfractures. Typical stress-strain curves (right) are shown for increasing confining pressures; differential stress is the principal maximum stress σ1 minus the minimum stress σ3. The steep part of each curve (parallel to the green line) is the initial, recoverable elastic response; beyond this limit the curves represent permanent deformation. From Middleton and Wilcock 1974, Figure 4.8 — A schematic of a typical experimental set-up for triaxial tests on rock samples. Confining pressure is increased by increasing the pressure on the oil surrounding the jacketed rock cylinder. The example of sheared rock shows fracture planes that are highly irregular, plus subordinate microfractures (from **R. Weijermars 2023**, Principles of Rock Mechanics, Figure 6.11b. Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. PDF available). Typical stress-strain curves (right) are shown for increasing confining pressures; differential stress is the principal maximum stress σ1 minus the minimum stress σ3. The steep part of each curve (parallel to the green line) is the initial, recoverable elastic response; beyond this limit the curves represent permanent deformation. From **Middleton and Wilcock 1974**, Figure 4.8

Failure at very low confining pressures commonly produces fractures that parallel the rock cylinder. At higher confining pressures conjugate fractures form where the conjugate set is approximately bisected by the maximum principal normal stress σ₁. Theoretically the two fracture planes should form at angles where the shear stress is a maximum, in other words at 45^o to σ₁. The fracture angle (θ) is measured from σ₁ to the normal to the fracture plane. The reason for this is that the stress acting on the plane can be resolved into a normal stress component at right angles to the plane, and a component parallel to the plane which is the shear stress. Based on experiment, (θ) measured in this way tends to be slightly larger than 45^o (which means the fractures are aligned slightly less than 45^o either side of σ₁). Furthermore, it has been determined experimentally that the normal stress (piston pressure) required for sample failure increases with increasing confining pressure, but the fracture angle for a particular material (θ) remains relatively constant.

Examples of the stress-strain relationship for triaxial test failure of different rock types, where strain is expressed as a percentage (strain has dimensions of L), and stress is the confining pressure. The graph also illustrates the increase in rock strength with increasing confining pressure. Modified slightly from From R. Weijermars 2023, Principles of Rock Mechanics, Figure 6.10. op cit.

Coulomb’s statement of material failure

The experimentation and theory that established the principles of rock strength and criteria of failure are commonly attributed to Charles Augustin Coulomb (1736-1806) although his initial research drew on the work of two illustrious predecessors – Leonardo da Vinci (1452-1519) and Guillaume Amonton (1663 –1705). Both conducted experiments on friction; of significance to Coulomb’s later work was their conclusion that frictional forces are proportional to the normal forces acting on a plane.

Amonton in 1699, expressed this relationship something like:

Frictional force/ σ_N = Tan φ

where σ_Nis the normal force, φ is the internal friction angle, and Tan φ is variously called the friction factor, or friction coefficient, commonly written as γ. Tan φ is dimensionless. The internal friction angle is defined as the angle between the normal stress and resultant stress at the point of failure. The ‘internal’ part of the name refers to friction forces within a material – forces that resist deformation, rather than friction on a surface.

[Note the difference between the internal friction angle φ, and the angle of fracture θ that references an actual, observable fracture plane – they are not the same measure.]

Coulomb recognized the importance of friction as a control on material failure. However, he concluded that the natural strength, or cohesion of rock, sediment, and soil also played a critical role (Coulomb, 1773). His mathematical statement expands Amonton’s equation such that the shear stress (τ) at the point of material failure requires a cohesive strength term and a friction term, thus:

τ = C₀ + Tanφ σ_N or

τ = C₀ + σ_N γ

where τ is the shear stress at the point of failure and C₀ is the material cohesive strength. This is the iconic Coulomb criterion for material failure.

A useful way to visualize the internal friction angle (φ) is to conduct a simple experiment demonstrating the angle of repose for a pile of dry, well-sorted sand; the actual value is about 34^o. If the slope increases it becomes gravitationally unstable and grains will slide or tumble downslope until the repose angle is re-established – in other words, the granular material shears – the repose angle represents the condition of dry sand peak-strength at the point of failure. This basically is the model applied to failure of harder rock where internal shear is caused by differential stresses.

Plotting Coulomb’s criterion for failure

Coulomb’s statement τ = C₀ + Tanφ σ_Nis the equation of a straight line for a graphical plot of shear stress against normal stress – also called the failure envelope or Mohr-Coulomb envelope. The slope of the line gives the value of (φ); the intercept on the shear stress axis (τ) is C₀.

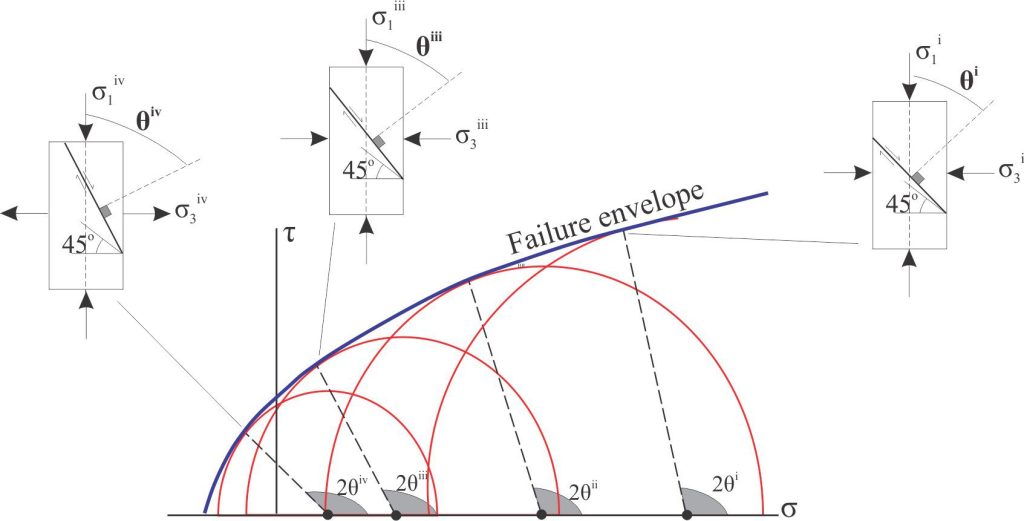
The two axes in the plot (shear stress τ and normal stress σ) are the same used to construct Mohr circles. Construction of the Mohr-Coulomb diagram for the failure conditions of a particular material makes use of experimental data obtained from the stress tests described above. The failure envelope makes a tangent to the Mohr circle at the point where the stress conditions for failure are represented (red dot in the diagram below). As noted previously, the orientation of the experimental fracture plane is designated θ – the angle measured from the normal to the fracture plane to σ₁. On the Mohr circle this is plotted as 2θ. In a conjugate fracture set there will be two failure envelopes – one at or close to the maximum positive shear stress, and the other the minimum negative shear stress.

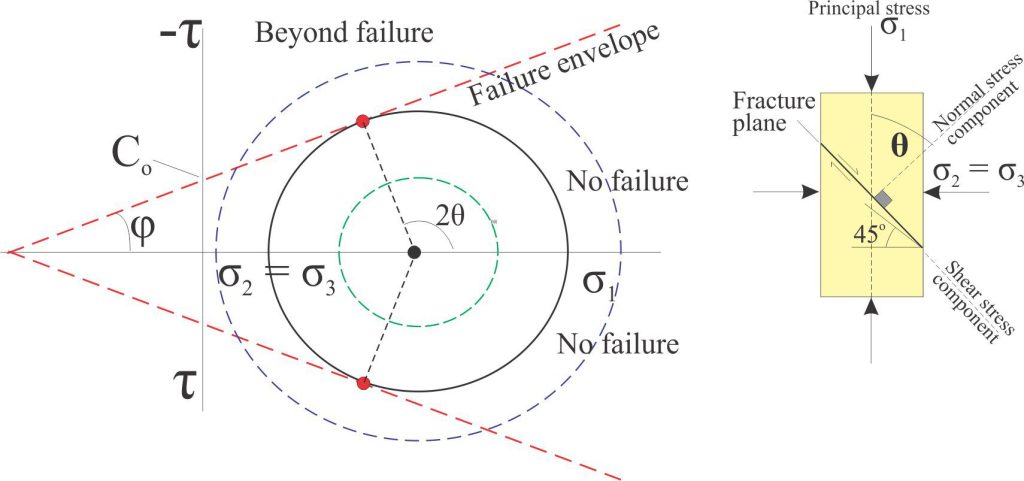
The Coulomb criterion for material failure, plotted as a straight line, is combined with a Mohr circle – in practice the stress values are determined experimentally. The straight line is a tangent to the circle at the point of failure. Co is cohesive strength, φ the internal friction angle, and θ-2θ the fracture plane orientation. The stress conditions below the line are insufficient to generate failure (green Mohr circle). Conversely, it is not possible for a Mohr circle (blue circle) to extend above the line because failure would occur before those stress conditions were reached. Note that the minimum and intermediate principal stresses are equal in both uniaxial and triaxial tests. The relationship between θ and σ1 is shown in the theoretical rock cylinder on the right.

Constructing a Mohr-Coulomb envelope

The starting point is measurement of the principal stress (σ₁) and confining pressures (σ₂ = σ₃) at the point of failure, and the experimentally derived fracture plane angle θ; the value of 2θ gives us the tangent to the Mohr circle. In practice, measurement of θ can be difficult because failure does not always occur along a single, coherent plane. To avoid this problem, it is common practice to perform several experiments on the same material and measure the principal stress (piston pressure) at different confining pressures. The rationale for this, as noted above, is that θ remains reasonably constant for different confining pressures. Mohr circles are constructed for each case and the line representing the best-fit tangent is drawn, giving us values of 2θ, φ, C_o, and shear stress at each point of material failure.

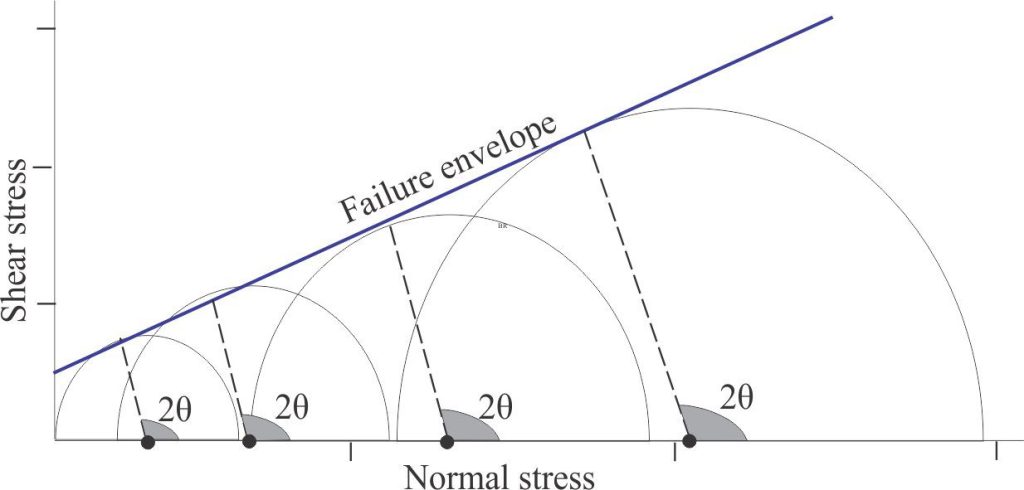
Construction of a best-fit tangent to Mohr circles that represent material failure at different confining pressures in a series of triaxial stress tests conducted on samples of the same rock type. The value of 2θ remains relatively constant in each stress test.

The non-linear case

For many cases of brittle deformation, the straight-line failure envelope is a good approximation of the conditions leading to fracturing. However, for some materials the failure angle is not a linear function of confining pressure – the result is a parabolic curve in which 2θ and φ are not constant with decreasing confining pressures. This is manifested as fracture planes that steepen towards σ₁ (i.e., the angle between σ₁ and the fracture plane decreases) whereas 2θ increases.